Homework 3

Problem 1.

The figure below shows a flow network along with a flow. In the figure, the notation \(a/b\) for an edge means that the flow on the edge is \(a\) and the capacity of the edge is \(b\).

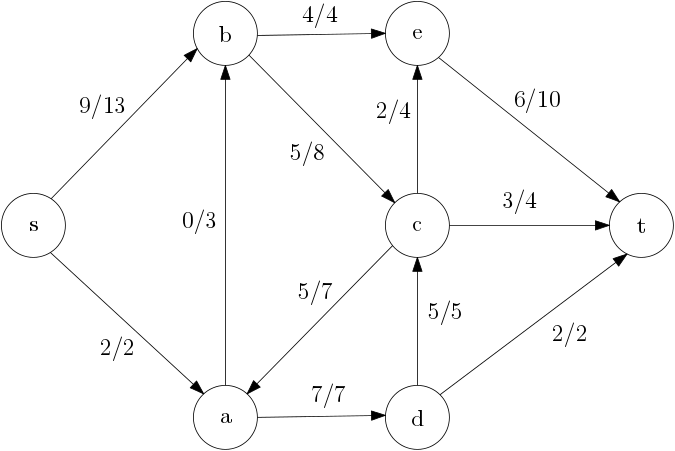
A flow network

Prove that this flow is not a maximum flow.
Give a minimum cut for this flow network, and
prove that your cut is indeed a minimum cut.

Problem 2.

Decide whether you think the following statement is true or false. If it is true, give a short explanation. If it is false, give a counterexample.

Let \(G\) be an arbitrary flow network, with a source \(s\), a sink \(t\), and a positive integer capacity \(c(u,v)\) on every edge \((u,v)\). If \(f\) is a maximum flow in \(G\), then \(f\) completely uses every edge out of \(s\) in \(G\) (that is, \(f(s,v) = c(s,v)\) for every vertex \(v \neq s\)).

Problem 3.

Decide whether you think the following statement is true or false. If it is true, give a short explanation. If it is false, give a counterexample.

Let \(G\) be an arbitrary flow network, with a source \(s\), a sink \(t\), and a positive integer capacity \(c(u,v)\) on every edge \((u,v)\). Let \((S, T)\) be a minimum cut in this network. Now suppose we add \(1\) to every capacity (that is, we increase each capacity by one). Then \((S, T)\) is still a minimum cut with respect to the new capacities.

Problem 4.

Consider this problem from the Polish Olympiad in Informatics:

A team of speleologists organizes a training in the Great Cave of Byte Mountain. During the training each speleologist explores a route from Top Chamber to Bottom Chamber. The speleologists may move down only, that is the level of every consecutive chamber on a route must be lower than the previous one. Moreover, each speleologist has to start from Top Chamber through a different corridor and each of them must enter Bottom Chamber using a different corridor. The remaining corridors may be traversed by more than one speleologist. How many speleologists can train simultaneously?

Explain how to solve this problem using max-flow. (Follow the link above for a more precise problem statement.)

Problem 5.

As a child, you may have played with cubes carrying six letters on their six faces. For instance, if you have one cube with the letters ABCDEF, one cube with the letters GHIKLM, and on cube with the letters NOPRST, you can make the word DOG, but not the word CAT (because you cannot use C and A from the same cube).

Given a description of \(n\) available cubes and a word with \(k\) letters, explain how to use max-flow to determine if the word can be spelled with the cubes.

(You can also find this problem on Topcoder.)