Programming project 2

Download the archive pp2.zip. It contains all the files for this project.

Recursive drawing

The file drawing.py contains a function draw_front that generates the following fractal drawing (shown here for levels 1, 2, 3, and 4):

Your task is to fill in the implementation of the three functions draw_order, draw_right, and draw_back.

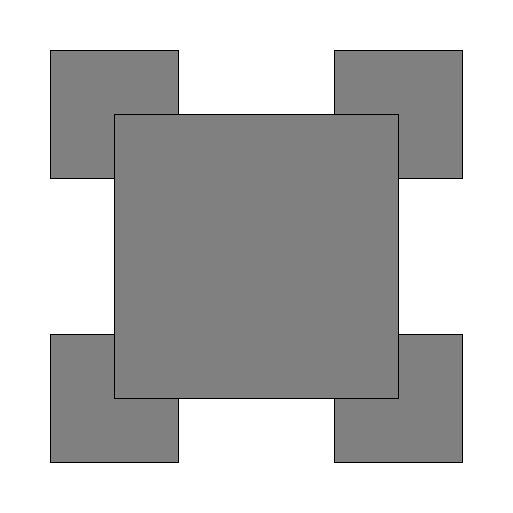
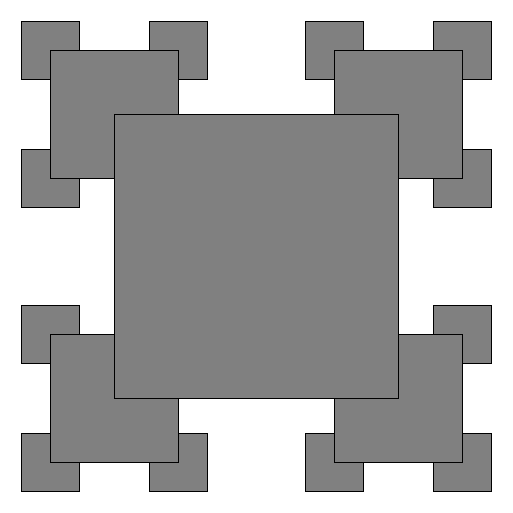
draw_order must produce the following drawing (again shown for levels 1, 2, 3, and 4):

draw_right must produce the following drawing: And draw_back must produce the following drawing: Submission: Upload your file drawing.py to the submission server.

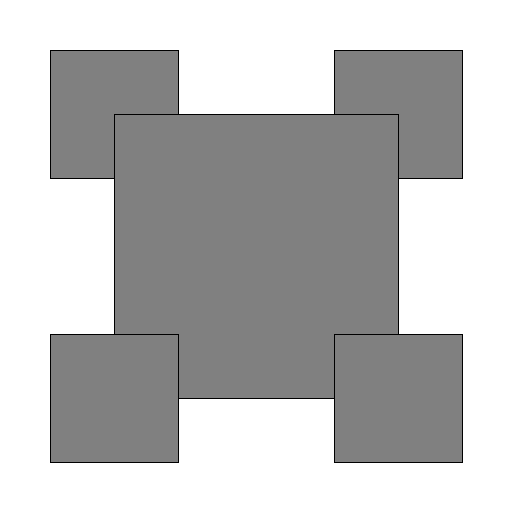
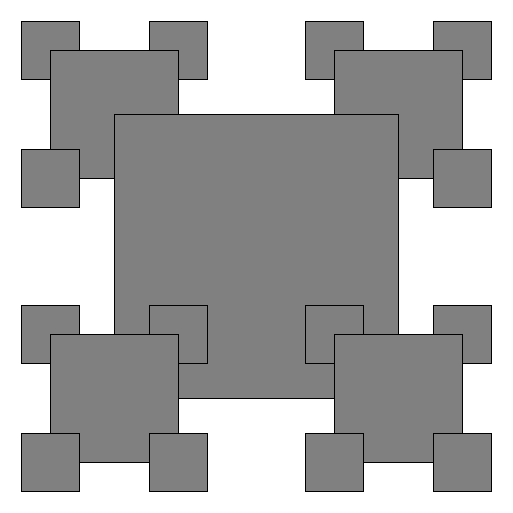
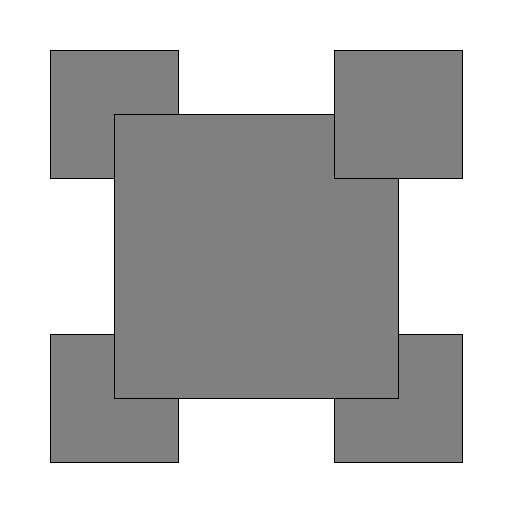
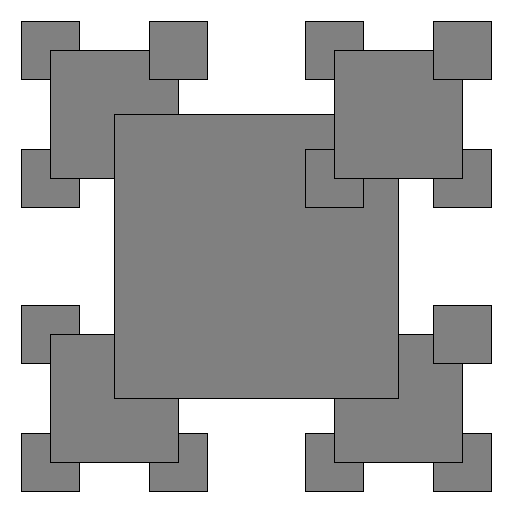
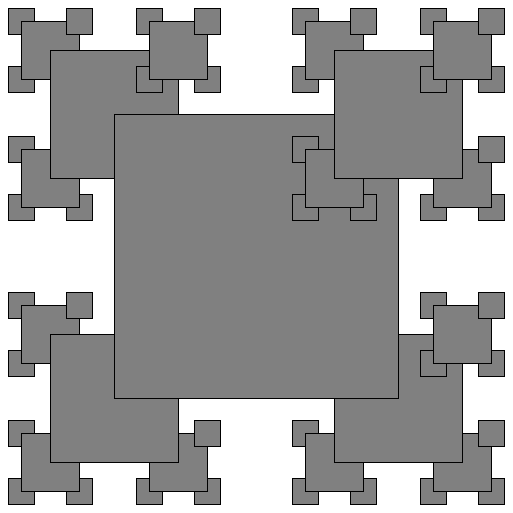
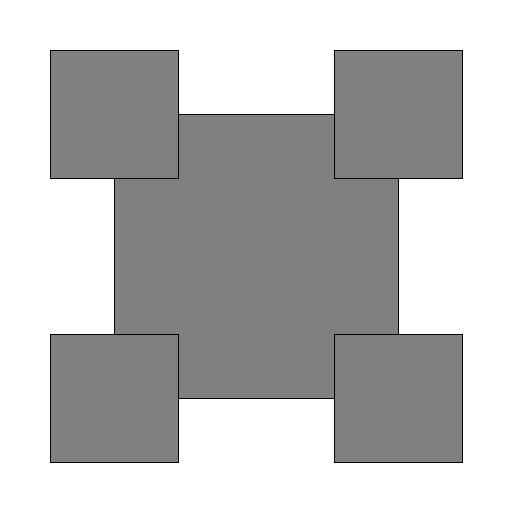
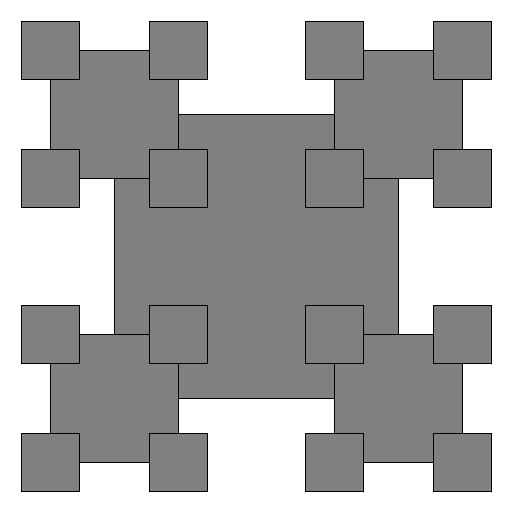
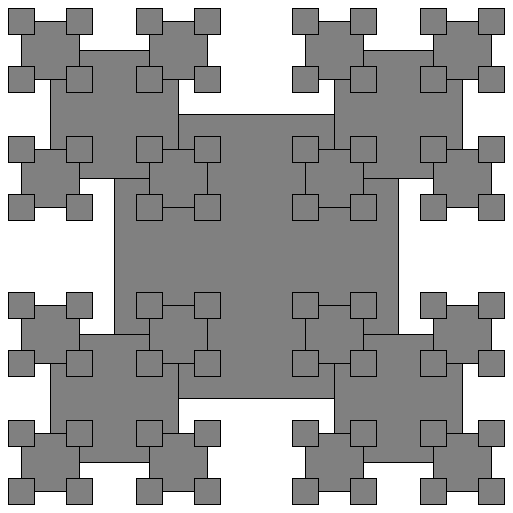
Sine and cosine

In our calculator program we learnt about indirect recursion, where function f calls function g, and function g calls function f (possibly with more levels in between). In this task we practice using indirect recursion:

Maybe you have wondered how functions like sin(x) and cos(x) are implemented in Python (and other programming languages). Here is one possible implementation. You know from high school or your calculus course that

and

Implement the functions sine and cosine in the file sine.py to use these indirectly recursive formulas.

The base case happens when \(x\) is very small, that is \(-0.01 < x < 0.01\). For such small values of x, use the approximations

and

The script already contains a tabulate function that tabulates your values of sine and cosine for \(x\) between \(-2\) and \(2\), with steps of \(0.1\), and compares your values with the result of the built-in functions math.sin and math.cos. How precise are your functions?

If you needed to improve the precision of your functions, how would you do it?

Submission: Upload your file sine.py to the submission server.

Towers of Hanoi, clockwise

Consider the following variant of the towers of Hanoi problem. As usual, we are given three pegs A, B, C. At the start, there are \(n\) disks on peg A. The problem is to move them all to peg B.

However, this time a disk can only move clockwise: from peg A to B, from peg B to C, or from peg C to A. All other moves are not allowed. For instance, it is not allowed to move a disk directly from peg A to peg C.

Of course all the other rules are still valid: You can only move the top disk on each pole, and a disk is not allowed to lie on top of a smaller disk.

Fix the implementation of the function hanoi_cw in the file clockwise.py (you can make additional functions, if you find them necessary). The current implementation is simply the original version of Towers of Hanoi (where counter-clockwise moves are allowed).

Like in the original version, your function should print the output using print statements in the following format:

Move disk 1 from A to B
Move disk 1 from B to C
Move disk 2 from A to B
Move disk 1 from C to A
Move disk 1 from A to B

This is actually a correct solution for \(n = 2\).

You must follow this format exactly, otherwise the unit tests will not accept your solution.

You can run the function directly from clockwise.py:

$ python3 clockwise.py 3

The script test_clockwise.py implements unit tests for hanoi_cw. It tests that the output is correct for a number of different values of \(n\), and prints out the number of moves used.

You will achieve partial credit for this problem if your solution works with the following number of moves (or better):

$ python3 test_clockwise.py 
For 1 disks you needed 1 moves
For 2 disks you needed 5 moves
For 3 disks you needed 21 moves
For 4 disks you needed 85 moves
For 7 disks you needed 5461 moves
For 10 disks you needed 349525 moves
.
----------------------------------------------------------------------
Ran 1 test in 1.202s

OK

For full credit, however, you need to achieve the following number of moves (this is harder):

$ python3 test_clockwise.py 
For 1 disks you needed 1 moves
For 2 disks you needed 5 moves
For 3 disks you needed 15 moves
For 4 disks you needed 43 moves
For 7 disks you needed 895 moves
For 10 disks you needed 18271 moves
.
----------------------------------------------------------------------
Ran 1 test in 0.070s

OK

You will get bonus points if you can beat this solution.

Submission: Upload your file clockwise.py to the submission server.